¿Cómo se relaciona la distancia de enfoque con el tamaño del sujeto y la focal?
Pretendemos deducir la expresión que liga la distancia de enfoque d con la focal f del objetivo cuando se mantienen el tamaño del sujeto H y tu tamaño aparente en la imagen h.
Llamaremos m al grado de ampliación del sujeto, es decir la relación sobre su tamaño aparente en la imagen (h) y su tamaño real (H).
En fotos macro (tomadas a pequeña distancia) m es mayor que la unidad (los sujetos tienen mayor tamaño en la imagen del sensor que en la realidad), mientras que en fotos de sujetos tomados a distancia grande m es menor que la unidad (los sujetos tienen menor tamaño que en la realidad), siendo esta última la situación habitual.
Como en nuestro caso los tamaños del sujeto y su tamaño en la imagen se mantienen, el grado de ampliación m también se mantiene.
En este artículo en inglés de la wikipedia se proporcionan las ecuaciones fundamentales sobre el comportamiento de una lente simple y las relaciones entre los tamaños de imagen.
De dicho artículo se han tomado las ecuaciones y las imágenes mostradas.
El grado de ampliación se define como la relación entre el tamaño del sujeto en la imagen (h) y su tamaño real (H): \(m=\frac h H\)
Si observamos en el esquema el rayo que pasa por el centro de la lente, se forman dos triángulos semejantes a ambos lados de la imagen, de manera que:
\[m= \frac h H= \frac v s\]
Así pues, el factor de ampliación está también relacionado con las distancias entre el plano de enfoque y el plano de la lente (v) y entre el sujeto y el plano de la lente (s). Podremos despejar la distancia sensor (v) en función de la distancia al sujeto y el factor de ampliación (m):
\[v= m s\]
e introduciéndolo en la ecuación de la lentes simple obtendremos s:
\[\begin{split}& \frac 1 s + \frac 1 v = \frac 1 f \rightarrow \frac 1 s + \frac 1 {m s} = \frac 1 f \\ & s=\frac {m+1} m f \\ & v= (m+1)f \end{split}\]
Como la distancia al sujeto es la suma de las distancias del plano de la lente al plano de imagen y al sujeto, tendremos:
\[d=s+v\rightarrow d=(m+1)s\]
Utilizando la ecuación anteriormente obtenida que liga s con f, obtendremos la expresión definitiva:
\[ d= \frac {(m+1)^2} m f \]
En consecuencia la distancia de enfoque es proporcional a la focal utilizada f, dependiendo exclusivamente de ella y del grado de ampliación m.
Por tanto si con una focal de 50 mm enfocamos a una distancia d, con una de 100 mm tendremos que situarnos a una distancia doble (2d) para conseguir el mismo encuadre.
La relación entre la distancia necesaria para el encuadre (d1) con una focal f1 y la necesaria (d2) con una focal f2 será pues una simple relación lineal:
\[d_2= \frac {f_1} {f_2} \cdot d_1\]
Estudio de la evolución de las distancias de enfoque, al sujeto y a la imagen en función del encuadre.
Si las expresiones anteriores que relacionan la distancia de enfoque y distancia a la imagen las dividimos por la distancia focal del objetivo, obtendremos números adimensionales que hemos dado en llamar distancias normalizadas (en relación a la focal del objetivo empleado):
\[\frac s f = \frac {m+1} m; \frac v f = m+1; \frac d f =\frac {(m+1)^2} m\]
En la siguiente gráfica podemos ver dichas distancias normalizadas en función del factor de ampliación.
La distancia a la imagen (v) es siempre lineal en todo el rango del factor de ampliación.
Sin embargo, la distancia al sujeto y por tanto la distancia de enfoque, tienen un comportamiento diferente para valores de ampliación inferiores a la unidad (fotografía normal) y superior a la unidad.
Al análisis de la distancia de enfoque en macrofotografía le hemos dedicado otro artículo específico.
Nos centraremos pues en la evolución de las distancias para valores menores que la unidad.
En la fotografía normal, más que el factor de ampliación, se suele utilizar el tamaño del sujeto H.
Si lo normalizamos por el tamaño que se desea para su imagen h (que será la dimensión del sensor si queremos que ocupe toda la imagen), obtendremos H/h que es el valor inverso de m (1/m) .
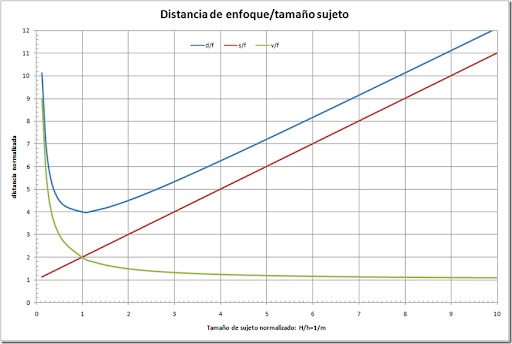
Así si representamos las distancias para valores de m < 1 en función del tamaño del sujeto normalizado (1/m > 1), obtendremos la gráfica siguiente.
Representemos con mayor detalle los valores correspondientes a tamaño de sujeto pequeño.
Vemos que para tamaños de sujeto normalizados grandes, la distancia a la imagen es casi constante e igual a la focal del objetivo (el objetivo enfoca en un plano a una distancia ligeramente por encima de su distancia focal).
Para tamaños de sujeto superiores a 2 la distancia a la imagen es inferior a 1,5 veces la focal del objetivo.
La distancia al sujeto es siempre lineal con el tamaño del sujeto, pues se puede expresar como:
\[s=(1+\frac 1 m)f\]
Las distancias de enfoque, para tamaños de sujeto grandes (superiores a 2), será prácticamente lineal, pues es la suma de la distancia al sujeto y a la imagen.
Para tamaño de sujeto 1 (igual al tamaño de la imagen proyectada), las distancias al sujeto y a la imagen son de dos veces la focal, y la distancia de enfoque es de cuatro veces la focal.
Por consiguiente, si queremos sacar un sujeto a su tamaño real (en el sensor) tendríamos que colocar dicho sujeto a una distancia 4 veces superior a su distancia focal. Por ejemplo, con un objetivo de 50 mm tendremos que enfocar a 20 cm.
Esa será la distancia mínima absoluta del objetivo, ya que no será capaz de enfocar objetos situados a menor distancia de 4f, siendo a esa distancia iguales las distancias a la imagen y al sujeto, que se sitúan a 2f.
Para distancias de enfoque mayores, el enfoque normal se produce reduciendo la distancia a la imagen (acercando la lente al plano de la imagen que se situará entre 2f y f) de manera que la distancia al sujeto aumenta (por encima de 2f), y se obtiene un factor de ampliación menor que la unidad.
El procedimiento de enfoque en macro es justo lo contrario, pero eso, junto con el comportamiento de la distancia de enfoque a distancias de macro lo estudiaremos en el artículo del enfoque en macrofotografía.
Conclusiones:
- La distancia de enfoque, la del sujeto y la de la imagen son proporcionales a la focal utilizada.
- Por consiguiente, para mantener el encuadre, si aumentamos la focal hemos de alejarnos del sujeto proporcionalmente, es decir: para fotografiar el mismo sujeto con una focal de 100 mm hemos de colocarnos al doble de distancia del sujeto que con una focal de 50 mm.
- Un objetivo nunca es capaz de enfocar el sujeto a distancias inferiores a 4 veces la focal del objetivo.
- En un objetivo normal, el enfoque se produce acercando la lente al plano de imagen, moviéndose la distancia a la imagen v entre f y 2f.
- En el enfoque normal de un sujeto de tamaño grande en relación a la imagen, la distancia normalizada de enfoque a la que hemos de situarnos es aproximadamente proporcional al tamaño del sujeto.
Archivos de descarga:
Archivo Excel para el cálculo de la Distancia de enfoque.


Comentarios