¿Se reduce la profundidad de campo al utilizar objetivos de mayor distancia focal manteniendo el mismo encuadre?
Todos hemos oído que la profundidad de campo de un teleobjetivo es más reducida que la de un angular.
Cuando hacemos un retrato, nos recomiendan utilizar un teleobjetivo y acercarnos lo posible al sujeto para reducir la profundidad de campo.
Pero ¿es esto realmente así? ¿por qué se reduce la profundidad de campo si es que lo hace?
Evidentemente nadie discute que la profundidad de campo disminuye cuando (manteniendo el resto de parámetros) aumenta la distancia focal.
Tampoco que la profundidad de campo sea más pequeña cuando la distancia al sujeto se reduce (manteniendo el resto de parámetros).
Pero es que no es esa exactamente la situación a que nos enfrentamos cuando estamos realizando un retrato.
Si realizamos un retrato con un objetivo de 50mm de manera que la la cara de la persona retratada llene casi todo el encuadre, tendremos que ponernos a una distancia determinada.
Si seguimos el consejo de usar un tele para que la profundidad de campo sea más reducida, escogeremos un 100 mm por ejemplo. Pero si nos ponemos a la misma distancia, le sacaremos sólo la parte de los ojos. Así que tendremos que alejarnos más para conseguir tener el mismo encuadre que con el objetivo de 50mm.
Pero al alejarnos, la profundidad de campo aumentará porque ahora estamos más lejos del sujeto.
¿Qué predomina el aumento de profundidad de campo por habernos alejado del sujeto o la disminución de profundidad de campo al utilizar una focal más larga?
Esa pregunta es la que queremos dilucidar en este artículo.
Planteemos para ello claramente los supuestos.
Queremos estudiar la influencia sobre la profundidad de campo de la focal del objetivo cuando mantenemos el mismo encuadre sobre el sujeto y utilizamos la misma apertura de diafragma (que en un retrato será normalmente la máxima que permite el objetivo).
Llamaremos en este estudio H a la dimensión del sujeto que queremos encuadrar y h a la dimensión del sensor con el que realizamos la toma (o al tamaño que queramos que tenga en la imagen tomada, medida en el sensor).
El encuadre de la foto queremos que sea el mismo, luego pretendemos que el valor de H y de h se mantengan.
Llamaremos f a la focal del objetivo y DOF a la profundidad de campo, diferencia entre el plano focal más alejado que se puede considerar correctamente enfocado y el plano más cercano a la cámara que se pueda considerar correctamente enfocado.
Replanteando nuestra pregunta con formulación matemática, lo que queremos estudiar pues, es cómo varía DOF en función de f cuando mantenemos tanto H (tamaño del sujeto) como h (tamaño de su imagen sobre el sensor).
Iremos para ello respondiendo a diversas preguntas.
¿Cómo se relaciona la distancia de enfoque con la focal del objetivo cuando mantenemos el encuadre?
Pretendemos deducir la expresión que liga la distancia de enfoque d con la focal f del objetivo cuando el encuadre del sujeto (es decir, su grado de ampliación m)
En este artículo de las guías fotográficas, hemos deducido la expresión que liga esas tres magnitudes, tal y como se muestra a continuación.
El grado de ampliación m vendrá dado por:
\[m= \frac h H\]
Como hemos dicho, si pretendemos mantener el encuadre, tanto H como h se han de mantener y, por tanto, también su grado de ampliación.
La ecuación que liga la distancia de enfoque con el grado de ampliación y la focal (tomada del artículo mencionado) viene dada por:
\[d= \frac {(m+1)^2} m f\]
En consecuencia la distancia de enfoque es proporcional a la focal utilizada f, dependiendo exclusivamente de ella y del grado de ampliación m.
Por tanto si con una focal de 50 mm enfocamos a una distancia d, con una de 100 mm tendremos que situarnos a una distancia doble (2d) para conseguir el mismo encuadre.
La relación entre la distancia necesaria para el encuadre (d1) con una focal f1 y la necesaria (d2) con una focal f2 será pues una simple relación lineal:
\[d_2= \frac {f_1} {f_2} \cdot d_1\]
Veamos un ejemplo concreto.
Tomemos como referencia una cámara Canon EOS 300D. Esta cámara tiene como factor de multiplicación 1,6 (y todas las cámaras de formato APS-C de Canon).
El tamaño del sensor será pues de 15x22,5 mm.
Imaginemos que queremos sacar un retrato en formato horizontal a un objeto de 30cm de alto (como la cara de una persona) de forma que ocupe toda la imagen.
El grado de ampliación será m=15 mm/300 mm= 0,05.
Si utilizamos una focal de 50 mm, deberemos de situarnos a una distancia de 1,10 m.
Si utilizamos una focal de 100 mm, la distancia debería de ser el doble: 2,21 m.
Pongamos ahora un caso de fotografía macro. Imaginemos que queremos sacar una imagen de un objeto de 1 cm en formato vertical, de manera que ocupe toda la imagen.
El grado de ampliación sería: m= 15 mm/10 mm = 1,5.
La distancia de enfoque con un objetivo de 50 mm debería de ser en este caso de 20,83 cm.
Con un objetivo de 100 mm, la distancia de enfoque sería de 16,66 cm (suponiendo que ambos objetivos macro me permitieran enfocar a esas distancias tan cercanas).
| Distancia de Enfoque | Retrato | Macro |
| Objetivo 50 mm | 1,10 m | 20,83 cm |
| Objetivo 100 mm | 2,21 m | 41,67 cm |
Conclusión:
La respuesta a la pregunta que nos hacíamos es sencilla: la distancia de enfoque (manteniendo el encuadre) es proporcional a la focal utilizada, por tanto si usamos una focal doble de otra, la distancia a que nos debemos situar es del doble.
Otro análisis interesante de la misma ecuación, es ¿cómo evoluciona la distancia de enfoque en función del tamaño del sujeto o de su grado de ampliación?, pues la respuesta depende de si se trata de objetos de tamaño grande o de pequeño tamaño (macrofotografía).
¿Cómo varía la profundidad de campo al cambiar la focal cuando se mantiene el encuadre y la apertura de diafragma?
Llegamos ahora a la pregunta que nos hacíamos.
Según hemos visto en el apartado de profundidad de campo, ésta viene determinada por las siguientes expresiones:
\[D_F= \frac {sf^2} {f^2-Nc(s-f)};D_N=\frac {sf^2} {f^2+Nc(s-f)}\]
Pondremos ahora estas ecuaciones en función del factor de ampliación (m), teniendo en cuenta que
\(s= {\frac {m+1} m} f \) , expresión que hemos deducido en el artículo sobre el la relación entre distancia de enfoque y factor de ampliación.
\[D_F= \frac {(m+1)f^2} {mf-Nc};D_N=\frac {(m+1)f^2} {mf+Nc}\]
Y obteniendo la diferencia entre ambos valores, llegaremos a la expresión de la profundidad de campo en función de el grado de ampliación, la apertura de diafragma, el tamaño del círculo de confusión y la focal empleada.
\[DOF= D_F - D_N= (m+1)f^2 \left [ \frac 1 {mf-Nc} - \frac 1 {mf +Nc}\right ]= (m+1)f^2\frac {2Nc}{(mf)^2-(Nc)^2}\]
Y si simplificamos un poco más la ecuación obtenida, llegaremos al resultado definitivo:
\[DOF=\frac {2(m+1)}{m^2-(Nc/f)^2} N c \]
Dado que \(N= f/d_p\) (siendo \(d_p\) el diámatro de la pupila de abertura), el término \(N c /f= c/d_f\) es decir la relación entre el círculo de confusión y el tamaño real de la pupila de entrada.
Cuanto más grande sea esa relación, mayor será la profundidad de campo, puesto que el denominador disminuye.
Si dicha relación es pequeña (caso habitual donde la pupila de entrada es bastante grande en realación al círculo de confusión) la profundidad de campo alcanzará un valor mínimo límite dado por:
A medida que la focal crece, la profundidad de campo disminuye, tendiendo a un valor límite dado por:
\[DOF_{min}=\frac {2(m+1)}{m^2} N c\]
Este valor de la profundidad de campo a la que tiende cuando cerramos diafragma es independiente de la focal empleada.
Si pretendemos obtener la mayor profundidad de campo posible fijados en número de abertura, la ampliación y el círculo de coonfusión, hemos de minimizar el valor del denominador.
Con el denominador tendiendo a cero la profundidad de campo tenderá a infinito y la focal correspondiente habrá de ser:
\[f_{optima}= \frac {N c}{m}\]
Aunque este valor teórico obtenido para la focal nos da valores de focales excesivamente pequeños, por lo que tendremos que conformarnos con emplear focales cortas y números de abertura grandes para tratar de conseguir la mayor profundidad de campo posible.
El empleo de números de abertura excesivamente grandes producirá una pérdida de detalle debido a la difracción, luego el mayor número de abertura que podemos emplear estará limitado en función de la resolución necesaria en la imagen y cuándo el efecto de difracción empieza a hacerse notable para dicha resolución.
La difracción depende del tamaño físico de la pupila real.
Veamos un ejemplo concreto
Tomemos como referencia una cámara Canon EOS 300D, cuya resolución es de 6,1MP.
Calculemos la profundidad de campo de esa cámara para los dos casos anteriores: retrato de una persona u objeto de 30 cm de tamaño y fotografía macro de un objeto de 1 cm, para focales de 10,50,100 y 200mm y con aperturas de 1,4; 2,8; 8; 16 y 22mm.
El tamaño del pixel en esta cámara (calculado a partir de su resolución) es de 7,44 micras. Utilizaremos ese valor como tamaño del círculo de confusión. El tamaño del sensor es de 22,5x15 cm.
A partir de esos datos y de la formulación anterior, calculamos la Profundidad de campo que queda reflejada en la siguientes tablas:
Encuadre de objeto de 30 cm en horizontal, de forma que ocupe 22,5 cm en el sensor (factor de ampliación m=0,075)
| f/1,4 | f/2,8 | f/8 | f/16 | f/22 | |
| 10 mm | 39,811 cm | 79,667 cm | 228,887 cm | 446,642 cm | 656,741 cm |
| 50 mm | 39,803 cm | 79,608 cm | 227,503 cm | 455,350 cm | 626,669 cm |
| 100 mm | 39,803 cm | 79,607 cm | 227,460 cm | 455,006 cm | 625,774 cm |
| 200 mm | 39,803 cm | 79,606 cm | 227,449 cm | 454,920 cm | 625,550 cm |
| 1000 mm | 39,803 cm | 79,606 cm | 227,446 cm | 454,892 cm | 625,479 cm |
Encuadre de objeto de 1 cm en horizontal, de forma que ocupe 22,5 cm en el sensor (factor de ampliación m=2,25).
| f/1,4 | f/2,8 | f/8 | f/16 | f/22 | |
| 10 mm | 1,337 mm | 2,674 mm | 7,640 mm | 1,528 cm | 2,101 cm |
| 50 mm | 1,337 mm | 2,674 mm | 7,640 mm | 1,528 cm | 2,101 cm |
| 100 mm | 1,337 mm | 2,674 mm | 7,640 mm | 1,528 cm | 2,101 cm |
| 200 mm | 1,337 mm | 2,674 mm | 7,640 mm | 1,528 cm | 2,101 cm |
| 1000 mm | 1,337 mm | 2,674 mm | 7,640 mm | 1,528 cm | 2,101 cm |
Vemos pues que en macro (al menos con factores de ampliación grandes) la focal utilizada no tiene influencia ninguna en la profundidad de campo, que sí depende fuertemente de la apertura empleada.
Esto es lógico porque el valor de Nc/f es menor que la unidad y m es mayor que la unidad y por tanto el denominador es prácticamente m^2 para cualquier focal.
Como consecuencia en fotografía macro, podemos afirmar que la profundidad de campo no depende de la focal y que es proporcional a la apertura utilizada: si duplicamos la apertura, duplicaremos la PDC.
Evolución de la profundidad de Campo para apertura constante
Veamos la evolución más claramente, mediante ábacos en los que se muestre cómo evoluciona la PDC con el factor de ampliación y con la focal, manteniendo la apertura y el círculo de confusión.
Seguiremos utilizando la misma cámara anterior, con un círculo de confusión de 7,44 micras.
Para otra cámara habría que tener en cuenta que lo que importa es el valor de Nc, es decir, que si la cámara tiene un círculo de confusión doble de la del ejemplo, sus resultados serían equivalentes a haber utilizado una apertura mitad.
Sujetos de tamaño grande (factor de ampliación pequeño): Paisajes y arquitectura.
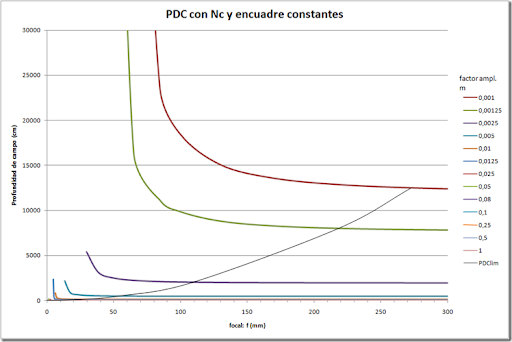
Gráfico para N=f/1,4 (Nc= 0,01041 mm) y factor de ampliación menor que la unidad.
Gráfico para N=f/8 (Nc= 0,0595 mm) y factor de ampliación menor que la unidad.
Gráfico para N=f/22 (Nc= 0,1636 mm) y factor de ampliación menor que la unidad.
La curva de color negro, con tendencia creciente, representa la focal a la que le corresponde una profundidad de campo un 5% mayor que la profundidad de campo mínima obtenida con focales muy largas.
Por tanto todas las focales superiores a la dada por dicha curva (a la derecha de curva) tendrán una profundidad de campo que se diferencia en menos del 5%, y por tanto la profundidad de campo será prácticamente igual.
Se observa claramente, que a medida que el factor de ampliación se hace más pequeño (es decir, sujetos más pequeños y que por tanto hemos de situarnos a menor distancia para encuadrarlos con una focal dada) la profundidad de campo crece rápidamente.
Además la caída de las curvas es menos brusca cuanto menor es el factor de ampliación.
Para sujetos de tamaño grande (factor de ampliación pequeño con distancia de enfoque elevada) la focal de la lente sí puede tener influencia en la PDC.
Con aperturas grandes, la influencia sobre la PDC es más pequeña, pero con aperturas cerradas, las curvas se hacen más suaves y por tanto la focal influye más en la PDC conseguida, reduciéndose progresivamente a medida que aumentamos la focal.
En cualquier caso hemos de notar que en esta situación la PDC es muy grande sea cuál sea la focal utilizada.
Sujetos de tamaño medio (factores ampliación medios): Retratos
Para tamaños de sujeto más pequeño los factores de ampliación son más grandes, y por tanto la influencia de la focal empleada es mucho menor.
Pongamos el caso de los retratos, donde el sujeto se puede mover en el orden de los 30 cm (retrato de un rostro) a 1,5 m (medio cuerpo o cuerpo entero), es decir factores de ampliación en el rango de 0,075 a 0,015.
Veamos las curvas ampliadas, en ese rango de factor de ampliación:
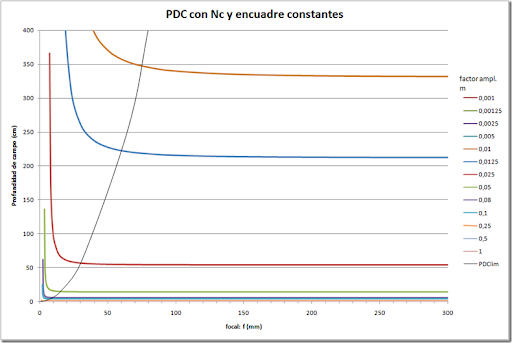
Gráfico para N=f/1,4 (Nc= 0,01041 mm) y factor de ampliación menor que la unidad.
Gráfico para N=f/8 (Nc= 0,0595 mm) y factor de ampliación menor que la unidad.
Gráfico para N=f/22 (Nc= 0,1636 mm) y factor de ampliación menor que la unidad.
Vemos que en retrato, incluso de cuerpo entero, focales por encima de 10 mm tienen prácticamente la misma PDC (al menos con aperturas grandes).
Con aperturas medias, la PDC la podemos considerar constante si empleamos una focal de 50 mm o más.
Únicamente con aperturas muy cerradas podremos notar diferencias en la PDC, en retratos de cuerpo entero y con focales de hasta 70mm.
Para retratos de rostro, o con focales de más de 70 mm, ni con las aperturas más cerradas notaremos diferencias en la PDC.
Además, en el caso de los retratos, normalmente buscaremos una PDC pequeña, por lo que utilizaremos aperturas grandes o medias.
Así que podemos concluir que la focal escogida no afecta prácticamente a la PDC conseguida en los retratos, siempre que comparemos fotografías tomadas con focales distintas pero en la que se mantiene el encuadre.






Comentarios